运动视差原理

运动视差原理：为什么近物跑得快，远物跑得慢

背景

今天早上送儿子上学的路上，儿子问了我这个问题，为啥我们坐在车上，看到近处的地面速度快，而远处的慢一些了，我隐约知道但是不太确认，所以使用deep search研究一下。

这篇文章是从通过天工超级智能体 deep Research研究生成的，这不是第一次使用deep Research了，现在感觉Deep Research是一个很有用的工具，特别是学习自己不了解的知识，我已经尝试过多次了，这次也没有让我失望。

引言：点出日常现象，引出核心问题

当我们乘坐汽车、火车等交通工具，目光投向窗外，常常会注意到一个有趣的现象：路边的树木、电线杆飞速向后掠过，而远处的群山、云朵则仿佛悠然自得，移动缓慢，甚至感觉相对静止。这种“近快远慢”的视觉体验几乎是每个人都曾有过的共同感受。那么，这背后究竟隐藏着怎样的科学原理呢？为什么我们的眼睛和大脑会这样感知物体的运动速度？

这种现象在科学上被称为运动视差（Motion Parallax）。它不仅仅是一种有趣的日常观察，更是我们视觉系统感知深度、理解三维空间的重要机制。本文将从物理学和视觉感知的角度出发，结合直观的解释、数学公式的推导以及生动的实例，深入剖析运动视差的成因，揭示“近快远慢”这一视觉奥秘。

一、视觉楔子：运动视差与角速度的核心关联

要理解为什么近处的物体看起来跑得快，远处的物体跑得慢，我们首先需要明确两个核心概念：运动视差本身，以及我们大脑是如何感知“速度”的。

1. 什么是运动视差（Motion Parallax）？

运动视差是指当观察者自身发生位移时，视野中处于不同距离的物体，在观察者视网膜上成像的相对移动速度存在差异的现象。具体来说，距离观察者较近的物体，其在视网膜上的投影移动得更快、幅度更大；而距离较远的物体，其投影移动得更慢、幅度更小。 [CSDN博客: Motion Parallax运动视差] 中提到：“Motion Parallax运动视差是一种深度视觉暗示，当我们运动时，会发现离我们近的物体运动的快，离我们远的物体运动慢一些。” [ScienceDirect Topics: Motion Parallax] 也指出：“Motion parallax refers to the fact that objects moving at a constant speed across the frame will appear to move a greater amount if they are closer to an observer (or camera) than they would if they were at a greater distance.” 这种现象是人类（以及许多动物）感知物体远近、构建三维空间感的重要单眼线索（monocular cue），即仅凭一只眼睛也能感知到。

2. 感知的“速度”是什么？——角速度登场

一个至关重要的前提是：我们的大脑在判断物体运动快慢时，并非直接测量其真实的物理线速度（比如米/秒），而是感知该物体在我们的视野中扫过的角度变化快慢。这个物理量就是角速度（Angular Velocity）。

在一篇关于 [爱问: 在行驶的车辆中看窗外的静止物体都在向后退] 的讨论中，有用户解释道：“眼睛是以同样时间质点运动的角度来判断运动‘速度’的，同样的时间里，近的物体移动角度大，而远的物体移动同样的距离角度小，因而显得近快远慢。” 类似地，[人人都是产品经理: 信息层级的新维度：视差运动] 一文中也指出：“人眼判断一个物体的快慢并不是以大地为参照物，而是以我们人眼本身为参照物……人眼感知的速度是夹角AOB的角度/时间。”

因此，理解“近快远慢”的关键，就在于分析不同距离的物体在我们视野中产生的角速度有何不同。

3. 距离如何影响角速度？

基于角速度是感知快慢的核心，我们可以初步推断：当观察者以一定速度运动时，在相同的时间间隔内，观察者相对于外界物体的空间位置发生了变化。

• 对于近处的物体，观察者视线方向的改变角度（即视角位移）会比较大。
• 对于远处的物体，即使观察者移动了相同的距离，其视线方向改变的角度也会小得多。

由于角速度定义为单位时间内的角位移，因此，视角位移大的近处物体，其感知角速度就大，显得运动快；视角位移小的远处物体，其感知角速度就小，显得运动慢。这便是运动视差现象的直观解释。

关键要点小结

• 运动视差：观察者移动时，不同距离物体在视网膜上相对运动速度的差异。
• 感知核心：人眼感知物体运动快慢主要依据其角速度，而非线速度。
• 距离效应：近物视角变化大，角速度大（感觉快）；远物视角变化小，角速度小（感觉慢）。

二、深入物理：参考系、相对运动与视角变化

为了更精确地理解运动视差，我们需要引入一些基础的物理学概念，如参考系和相对运动，并进一步分析视角是如何随距离变化的。

1. 选择正确的参考系

物理学中，描述运动首先要选定参考系。正如 [IT之家: 关于参考系与惯性系，你明白了吗？] 所述：“作为研究物体运动时所参照的物体。” 当我们坐在行驶的汽车上观察窗外景物时，我们自然而然地以自身（或汽车）为参考系。在这个参考系中，原本静止于地面的树木、房屋等，都在相对于我们向后运动。

2. 相对线速度的理解

假设汽车的速度为 v（例如，60公里/小时）。对于地面上静止的物体（如一棵树）而言，它相对于汽车的线速度大小也是 v，但方向与汽车前进方向相反。也就是说，如果我们认为自己是静止的，那么这棵树正以速度 v 向我们身后退去。这个相对线速度是后续分析角速度的基础。

3. 核心剖析：视角变化与距离的数学关系 (定性到初步定量)

现在，让我们构建一个简化的物理模型来分析视角变化。假设观察者（我们）正沿着一条直线以恒定速度 v 运动（即车速）。我们同时观察一个与我们运动路径垂直距离为 d 的静止物体P。

在一段极短的时间 Δt 内，观察者移动的距离为 Δx = v * Δt。在这段时间内，物体P相对于观察者的视线方向会发生一个角度变化，我们称之为视角变化 Δθ。

• 当物体P距离我们较近时（即 d 较小），要看清这个物体，我们的视线需要转动一个较大的角度 Δθ。
• 当物体P距离我们较远时（即 d 较大），即使我们移动了同样的距离 Δx，我们的视线转动的角度 Δθ 也会小得多。

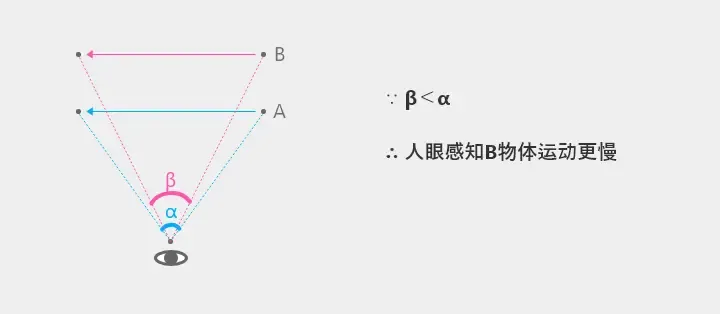上图直观地展示了这种几何关系：对于相同的观察者位移，近处物体对应的视角变化（其文中的夹角α）要大于远处物体对应的视角变化（其文中的夹角β）。

对于相同的观察者位移，近处物体对应的视角变化（其文中的夹角α）要大于远处物体对应的视角变化（其文中的夹角β）。

三、量化分析：角速度的计算与比较 (核心内容)

现在，我们将运用数学工具来精确计算和比较不同距离物体的感知角速度。这是从根本上解释“近快远慢”现象的关键一步。

1. 角速度 (Angular Velocity) 的定义与公式

角速度 ω (omega) 是描述物体转动快慢的物理量，定义为单位时间内转过的角度（角位移）。如果物体在 Δt 时间内转过了 Δθ 角度（以弧度为单位），则其平均角速度为：

ω = Δθ / Δt

这个公式来源于 [GeeksforGeeks: Angular Speed Formula] 等基础物理学知识。

2. 推导运动视差场景下的角速度公式

让我们回到之前建立的模型：观察者以速度 v 沿直线运动，观察一个与其初始位置垂直距离为 d 的静止物体P。

为简化推导，我们考虑物体P恰好经过观察者正侧方（即观察者视线与运动方向垂直的瞬间）附近极短时间 Δt 内的情况。在这段时间内，观察者向前移动了距离 Δx = v * Δt。物体P相对于观察者向后“移动”了近似相同的距离（在垂直于初始视线的方向上）。

此时，视线方向的变化角度 Δθ 可以通过几何关系近似得出。如下图所示，观察者的位移 Δx、物体距离 d 和视角变化 Δθ 构成一个近似的直角三角形（当 Δθ 足够小时）。

图 S2：角速度推导的简化几何模型。（此图为概念示意）

根据三角函数，我们有：tan(Δθ) = Δx / d = (v * Δt) / d。

由于是在极短时间内，Δθ 非常小，这时可以用小角度近似：tan(Δθ) ≈ Δθ (当 Δθ 以弧度为单位时)。 所以，Δθ ≈ (v * Δt) / d。

将此 Δθ 代入角速度的定义公式 ω = Δθ / Δt，可得：

ω ≈ ((v * Δt) / d) / Δt = v / d

其中：

• ω 是观察者感知到的物体的角速度 (rad/s)。
• v 是观察者自身的速度 (m/s) (或者说是物体相对于观察者的，垂直于视线方向的有效速度分量)。
• d 是物体到观察者运动路径的垂直距离 (m)。

这个简洁的公式 ω ≈ v / d 清晰地揭示了感知角速度与观察者速度和物体距离之间的关系。需要注意的是，这是一个简化模型下的近似结果，在物体并非恰好在正侧方或运动时间较长时，精确计算会更复杂，但其揭示的核心反比关系是成立的。许多分析，如 [Quora讨论]，也直接应用了类似 v = ω * r (即 ω = v / r) 的关系来解释这一现象。

3. 公式解读与“近快远慢”的定量解释

从核心公式 ω ≈ v / d 我们可以清晰地看到：

• 与速度 v 的关系：当物体距离 d 一定时，观察者（车辆）的速度 v 越大，感知到的角速度 ω 就越大，物体看起来运动得就越快。这符合我们的日常经验：车开得越快，窗外的景物掠过得也越快。
• 与距离 d 的关系：当观察者（车辆）的速度 v 一定时，感知到的角速度 ω 与物体到观察者路径的垂直距离 d 成反比。
  • 距离 d 越小（近处物体），分母小，ω 就越大，物体看起来运动得越快。
  • 距离 d 越大（远处物体），分母大，ω 就越小，物体看起来运动得越慢。
  • 当距离 d 趋向于无穷大时（例如远山、月亮、太阳），ω 趋近于零，这些物体看起来几乎是静止不动的。

这完美地从数学上解释了“近快远慢”的现象。

4. 计算实例与图表示例

为了更直观地理解，我们来看一个计算实例，并用图表展示其关系。

计算实例：

假设汽车行驶速度 v = 72 km/h。为了方便计算，我们将其转换为米/秒： v = 72 * 1000 m / 3600 s = 20 m/s。

• 近处的树木：假设其距离观察者路径的垂直距离 d_near = 10 m。 其感知角速度 ω_near ≈ v / d_near = 20 m/s / 10 m = 2.0 rad/s。
• 远处的山丘：假设其距离观察者路径的垂直距离 d_far = 2000 m (2公里)。 其感知角速度 ω_far ≈ v / d_far = 20 m/s / 2000 m = 0.01 rad/s。

比较两者：ω_near (2.0 rad/s) 远大于 ω_far (0.01 rad/s)，前者是后者的200倍！这清晰地从数量上展示了为什么近处的树木看起来飞速后退，而远处的山丘则几乎纹丝不动。

图表示例：

下面我们用图表来可视化这些关系。

图表1：不同距离物体的视角变化对比 (示意)

此图表旨在模拟在相同观察者位移（或相同时间Δt内）下，近处物体和远处物体产生的视角变化大小的对比。我们用条形高度来表示视角变化 Δθ 的相对大小。根据 Δθ ≈ (v * Δt) / d，Δθ 与 1/d 成正比。

图表2：感知角速度与距离的关系 (ω ≈ v / d)

此图表展示了在观察者速度 v 恒定（我们设定为 20 m/s）的情况下，感知角速度 ω 如何随物体距离 d 变化的函数曲线。

关键要点小结

• 核心公式：感知角速度 ω ≈ v / d。
• 定量解释：该公式表明，角速度与观察者速度 v 成正比，与物体距离 d 成反比，从而完美解释“近快远慢”。
• 实例佐证：计算表明近物角速度可远大于远物角速度，图表直观展示了这种差异和关系。

四、生活中的运动视差：更多实例与应用

运动视差不仅仅是我们在乘车时的一个有趣观察，它广泛存在于我们的日常生活中，并且在诸多科技领域有着重要的应用和启发。

1. 经典场景再现

除了最典型的乘坐汽车或火车的例子，运动视差在以下场景中也十分明显：

• 飞机上俯瞰大地：从万米高空俯瞰，即使飞机速度很快，地面上的景物移动也显得非常缓慢，这是因为距离 d 极大。而起飞和降落阶段，离地面较近时，地面景物的“运动”速度感就快得多。
• 跑步或骑行：在跑步或骑自行车时，路边的草丛、栏杆似乎快速向后闪去，而稍远一些的建筑则移动得慢一些。
• 观察星空：当我们转动身体（或地球自身在自转）观察星空时，月亮和遥远的星星几乎感觉不到它们的相对位置因我们的运动而改变，这是因为它们距离我们极其遥远，d 趋近于无穷大，使得 ω 极小。([知乎专栏: 10 个parallax 视差效果的网页范例] 中有类似描述)

2. 艺术与设计中的应用

运动视差的原理被巧妙地应用于视觉艺术和界面设计中，以增强作品的深度感和动态效果：

• 动画与电影特效：动画师和特效师常常利用运动视差来模拟三维空间的真实感。例如，在角色移动的场景中，背景的不同层面会以不同的速度卷动，前景快，中景次之，远景最慢，从而营造出强烈的空间纵深感。
• 网页与UI设计中的视差滚动（Parallax Scrolling）：这是一种流行的网页设计技术。当用户滚动页面时，背景图像的移动速度慢于前景内容，或者不同背景层以不同速度移动，从而创造出引人入mersive的3D效果和视觉趣味性。如 [博客园: 视差滚动技术的简介及运用] 所述，其原理就是在二维场景中创建一个深度错觉。 [人人都是产品经理: 信息层级的新维度：视差运动] 也强调了“分层、速度差和运动响应”是实现视差运动的核心。
• 视频游戏：尤其是在2D横版过关游戏中，运动视差是增强场景层次感和真实感的常用手段。不同景深的背景层以不同速率移动，使得平面的游戏世界显得更加立体。

3. 科技领域的启发与应用

运动视差的原理对于计算机视觉、机器人导航和虚拟现实等高科技领域具有重要的理论和应用价值：

• 计算机视觉与三维重建：通过分析摄像机（或机器人）运动时捕获的连续图像序列中，不同特征点的运动视差，计算机可以估算场景中物体的深度信息，进而重建三维场景。这是实现如SLAM（即时定位与地图构建）、自动驾驶车辆环境感知等技术的关键环节之一。例如，[知乎专栏: 视觉SLAM（一）] 提到：“当相机运动起来时，场景和成像有几何关系，近处的物体的像运动快，远处的物体的像运动慢，从而推断距离。”
• 深度估计：单目摄像头可以通过自身的运动，利用运动视差来估计与物体的距离，这对于无法使用双目摄像头或雷达等传感器的场景非常有用。
• 目标跟踪：运动视差信息可以帮助区分前景运动物体和背景，辅助系统更准确地跟踪特定目标。
• 虚拟现实 (VR) 与增强现实 (AR)：在VR/AR应用中，为了提供沉浸式和真实的用户体验，系统必须精确模拟头部运动所产生的运动视差。如果视差渲染不正确，不仅会破坏真实感，还可能导致用户眩晕不适。

可见，运动视差不仅解释了我们日常生活中的一个普遍视觉现象，其 underlying 原理更是在艺术创作和前沿科技中发挥着不可或缺的作用。

五、总结：洞悉视觉世界的动态奥秘

通过以上的分析，我们揭示了“近物跑得快，远物跑得慢”这一日常现象背后的科学机制——运动视差原理。其核心在于，我们对物体运动快慢的感知，主要取决于物体在我们视野中扫过的角速度，而非其绝对的线速度。

当观察者自身运动时，由于与物体的距离不同：

• 近处物体因其较小的距离 d，在相同时间内会在观察者视野中产生较大的视角变化 Δθ，从而导致较大的感知角速度 ω (ω ≈ v / d)，因此感觉运动快。
• 远处物体因其较大的距离 d，产生的视角变化 Δθ 则小得多，导致感知角速度 ω 较小，因此感觉运动慢，甚至在距离非常遥远时（如天体）趋于静止。

简洁的数学公式 ω ≈ v / d (其中 v 为观察者速度，d 为物体垂直距离) 精炼地概括了这一关系，为我们提供了定量的解释。

运动视差是人类视觉系统经过长期进化形成的一种高效感知深度和理解动态三维环境的重要机制。它不仅让我们能够判断物体的远近，还在艺术创作中被用来增强视觉效果，更在计算机视觉、机器人技术和虚拟现实等尖端科技领域扮演着关键角色。理解运动视差，不仅能满足我们的好奇心，更能让我们体会到物理规律与生物感知巧妙结合的奇妙之处，洞悉我们视觉世界中动态的奥秘。